[C++] 11407번 책 구매하기 3 - 최대 유량, 최소 비용 최대 유량

1. 문제

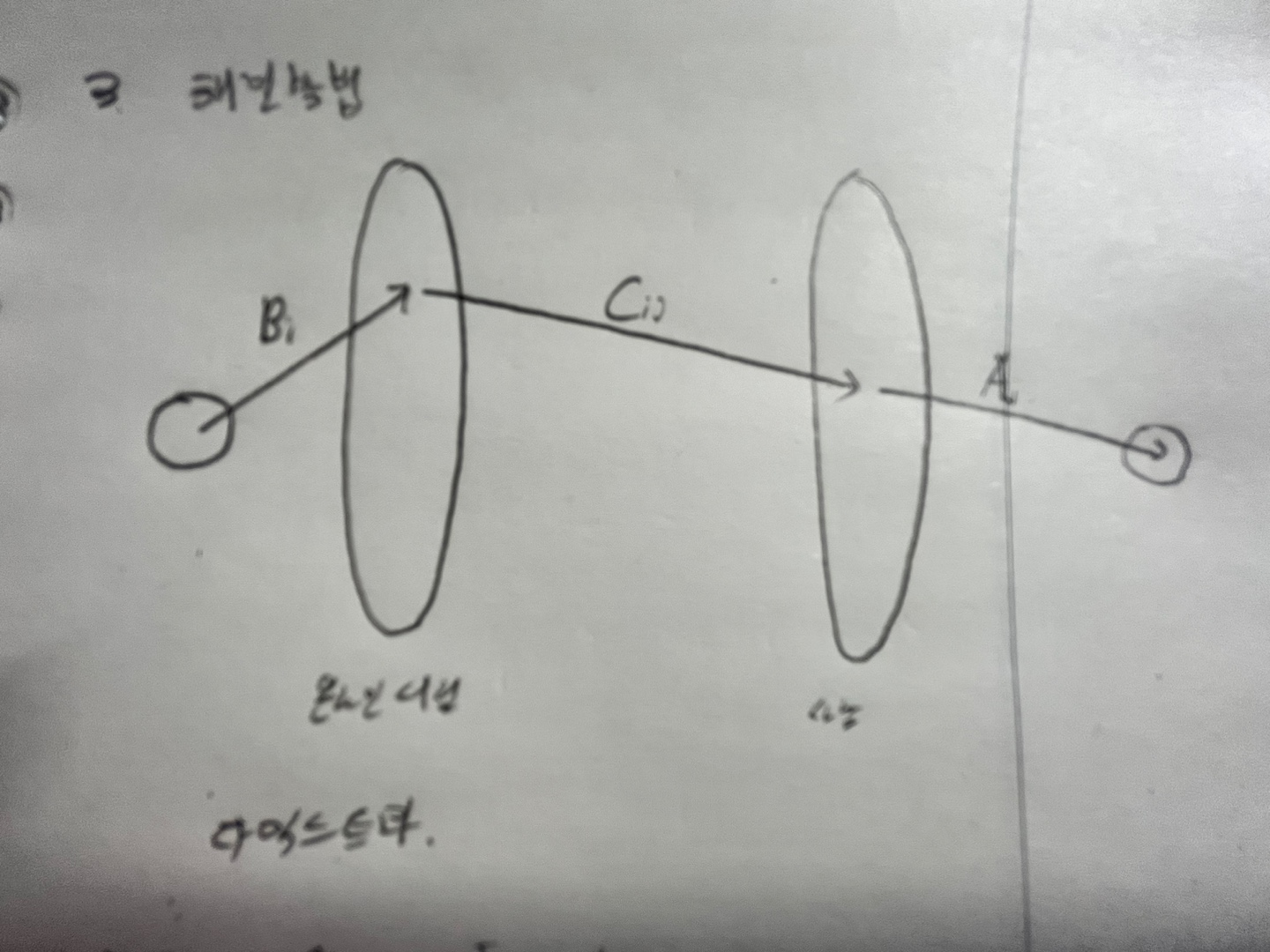
• N명의 사람이 책을 구매하려고 한다. 각 사람은 1~N번까지 번호가 매겨져 있고 각 사람이 사려고 하는 책의 개수는 Ai권이다. 이 책을 판매하는 온라인 서점은 M개가 있고 1~M번까지 번호가 매겨져 있으며, 각 서점이 가지고 있는 책의 개수는 Bi권이다.
• 서점에서 가지고 있는 책의 개수의 합과 사람들이 사고자 하는 책의 개수의 합은 같다.
• 한 사람이 같은 서점에서 구매할 수 있는 책의 최대 개수는 Cij이다. 온라인 수점에서 책을 한 권씩만 보낼 때 배송비는 Dij원이다.
• 살 수 있는 책의 최대 권 수와 그 때 배송비의 합의 최솟값을 구하는 프로그램을 작성하시오.

<입력>

• -1-   사람의 수 N, 온라인 서점의 수 M \(M(1 \leq N, M \leq 100)\)
• -2-   사람이 사려고 하는 책의 개수 Ai \((1 \leq A_{i} \leq 100)\)
• -3-   온라인 서점이 가지고 있는 책의 개수 Bi \((1 \leq B_{i} \leq 100)\)
• -M개-   온라인 서점 i에서 사람 j가 살 수 있는 책의 최대 개수 Cij \((0 \leq D_{ij} \leq 1,000)\)

<출력>

• -1-   살 수 있는 책의 최대 개수
• -2-   배송비 값의 최솟값

2. 재정의

• 온라인 서점에서 시작된 유량의 사람의 최대 유량을 구하고 이때 배송비 최솟값을 구하라.

3. 해결방법

방향 그래프

4. 실수한 점, 개선할 점

• 왼쪽에 있는 정점의 개수는 N개가 아닌 M개이다.
• 구조체를 이용하지 않고 배열을 이용하면 메모리는 더 많이 사용하는 대신 시간을 더 줄일 수 있다.
• 지금까지 최대 비용 최대 유량을 최대 유량 최소 컷 정리로 보고 있었다.

 

<코드>

#include <iostream>
#include <string.h>
#include <vector>
#include <queue>

using namespace std;

const int INF = 987654321;
const int MAX_N = 101;
const int MAX_M = 101;
const int MAX_V = 203;
const int HUMAN = 100;

// 간선 구조체
struct Edge {
    // next로 가는 용량이 capacity이고 유량이 flow인 가중치가 cost인 간선
    int next, capacity, flow=0, cost;
    Edge* rev;
    Edge(){}
    Edge(int _next, int _capacity, int _cost) : next(_next), capacity(_capacity), cost(_cost) {}
    
    // 흐를 수 있는 최대 유량
    int Remain() {
        return capacity - flow;
    }
    // 유량 흘려주기
    void Push(int x) {
        flow += x;
        rev->flow -= x;
    }
};
// 방향 그래프
vector<Edge*> adj[MAX_V];
// source와 sink
int S, E;

// 그래프 간선 생성하기
void makeEdge(int u, int v, int capa, int c) {
    Edge *uv = new Edge(v, capa, c), *vu = new Edge(u, 0, -c);
    uv->rev = vu, vu->rev = uv;
    adj[u].push_back(uv);
    adj[v].push_back(vu);
}

// 문제 조건
// 사람의 수 N, 온라인 서점의 수 M
int N, M;

/*
    사람이 사려고 하는 책의 개수 A[i]
    온라인 서점이 가지고 있는 책의 권수 B[i]
    온라인 서점 i에서 사람 j가 살 수 있는 책의 최대 권수 C[i][j]
    온라인 서점 i에서 사람 j에게 책을 보내는 데 필요한 배송비 D[i][j]
*/
int A[MAX_N], B[MAX_N], C[MAX_N][MAX_N], D[MAX_N][MAX_N];

// 최대 권수 total_flow, 최소 배송비 total_cost
int total_flow, total_cost;

void input() {
    cin >> N >> M;
    
    for(int i=1; i<=N; i++)
        cin >> A[i];
    for(int i=1; i<=M; i++)
        cin >> B[i];
    for(int i=1; i<=M; i++)
        for(int j=1; j<=N; j++)
            cin >> C[i][j];
    for(int i=1; i<=M; i++)
        for(int j=1; j<=N; j++)
            cin >> D[i][j];
}

void makeGraph() {
    S = 0, E = 201;
    
    // source와 온라인 서점 연결하기
    for(int i=1; i<=M; i++)
        makeEdge(0, i, B[i], 0);
    // 온라인 서점과 사람 연결하기
    for(int i=1; i<=M; i++)
        for(int j=1; j<=N; j++)
            makeEdge(i, j+HUMAN, C[i][j], D[i][j]);
    // 사람과 sink 연결하기
    for(int i=1; i<=N; i++)
        makeEdge(i+HUMAN, E, A[i], 0);
}

void MCMF() {
    while(1) {
        // 최대 유량 알고리즘 용 부모와 최단 거리
        int parent[MAX_V], dist[MAX_V];
        Edge *path[MAX_V];
        queue<int> q;
        
        // 배열 초기화
        memset(parent, -1, sizeof parent);
        fill(dist, dist+MAX_V, INF);
        
        // dfs
        dist[S] = 0;
        q.push(S);
        
        while(!q.empty()) {
            int here = q.front(); q.pop();
            
            for(auto e : adj[here]) {
                // 탐색할 곳
                int there = e->next;
                // 더 최단 경로가 존재할 경우 갱신
                if(e->Remain() > 0 && dist[there] > dist[here] + e->cost) {
                    dist[there] = dist[here] + e->cost;
                    parent[there] = here;
                    path[there] = e;
                    q.push(there);
                }
            }
        }
        // 더 이상은 증가 경로가 없으므로 종료
        if(parent[E] == -1)
            break;
        
        // 탐색한 경로로 흘려줄 수 있는 최대 유량
        int flow = INF;
        for(int p = E; p!=S; p = parent[p])
            flow = min(flow, path[p]->Remain());
        for(int p = E; p!=S; p = parent[p]) {
            total_cost += flow * path[p]->cost;
            path[p]->Push(flow);
        }
        
        total_flow += flow;
    }
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    
    input();
    
    // 그래프 만들기
    makeGraph();
    
    // 최대 유량 알고리즘 + 다익스트라
    MCMF();
    
    cout << total_flow << '\n' << total_cost;
    
    return 0;
}

 

 

<구조체를 이용하지 않은 코드(풀어야 볼 수 있습니다.)>

https://www.acmicpc.net/source/39238787

로그인

 

 

※현재 고등학교 등교 중인 학생입니다. 이제 알고리즘을 본격적으로 공부하기 시작해서 아직 초보입니다. 혹시 제가 잘못 알고 있는 점이나 더 좋은 풀이 방법이 있어 댓글에 남겨주시면 감사히 하나하나 열심히 읽어보겠습니다. 좋아요, 단순한 댓글 한마디라도 저에겐 큰 힘이 됩니다! 감사합니다.